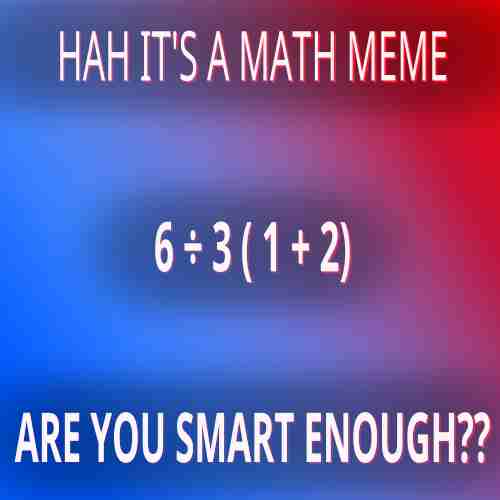1 - Algebra #
This section is a tad bit misnamed, as instead of covering just Algebra I’ll be covering most things you’d learn in a high school Algebra class along side it, plus probably a bit extra.
Number Systems #
To get started, let’s look at ‘Number Systems’. Essentially, there are a variety of ’types’ of numbers, rather than get all philosophical let’s just dive in and I think you’ll get the gist.
ℕ - Natural Numbers #
Natural Numbers are the dead basic set of numbers, 1, 2, 3, 4, 5, etc. note, this doesn’t include fractions, decimals, etc. or the number 0. Whole Numbers is the set of natural numbers and the number 0, so 0, 1, 2, 3…
ℤ - Integers #
Alright, Natural and Whole numbers are great and all, but what if we want to represent a deficit or debt? Negative numbers would definitely be nice- introducing Integers, this is just the set of Whole numbers and the their inverses, so -3, -2, -1, 0, 1, 2, 3 …
int types are bounded by how many bits they can store, for example, an 8 bit signed integer can only hold values ranging from -128 to 127.
ℚ - Rational Numbers #
Rational numbers are any numbers which can be written as an interger over another integer.
Of note, these can be written as mixed numbers too, that is \( \frac{4}{3} = 1\frac{1}{3} \) , as \( \frac{3}{3} = 1 \text{ so the remaining } \frac{1}{3} \) is just written next to it.
Note, that rational numbers do include numbers with an infinite repeating decimal, that is while \( \frac{1}{2} \text{ can be written as } .5 \) , \( \frac{1}{3} \text{ has a repeating decimal, } \frac{1}{3} = .333333... = .\overline{33} \) , where the line over the 3’s implies that the 3’s repeat infinitely. This is still a rational number.
- Irrational Numbers #
Alright then, what’s an irrational number?
Well, this is easier to answer with a few examples, the most well know of which is \( \pi = 3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499... \)
… I think you get the idea.
Irrational numbers are numbers where the decimal doesn’t repeat and as such can not be written as an integer over another integer. Because pi is a geometrically defined constant, it may be easier to look at something a bit more tangible.
The square root of a number is just the number that when multiplied with itself gives the number in question, so the square root of 4 is 2 because 2*2 is 4, the square root of 9 is 3 because 3*3 is 9, etc.
But what about the square root of 2? well \( \sqrt{2} = 1.414213562373.... \) you get the idea. Like with pi, it’s a number that goes on forever, with no repeating pattern.
Later on you’ll see other irrational constants like \( e = 2.718281828459.... \) and The Golden Ratio \( \frac{1+\sqrt{5}}{2} = 1.618033988749.... \)
ℝ - Real Numbers #
Finally, we’re up to the normal number line, that is, we now have the set of all numbers on the number line, all the way from -∞ to +∞, (often written as ±∞) pick any number, with as many random numbers before or after the decimal point as you want, and that’s a real number.
\( i \) - Imaginary Numbers #

Yep, that’s pretty much everyone’s first reaction. What in the hell is an imaginary number?
Well, okay, remember before how I said a square root was just whatever number you need to multiply with itself to get the number, so \( \sqrt{4} = 2 \) ? This has a problem, a negative number times a negative number is always positive, so \( 3 * 3 = 9, -3 * 3 = -9, \text{ but } -3 * -3 = 9 \) So, what would the square root of a negative number be? There are no two numbers that can multiply to give us -1, so, we made one up! \( \sqrt{-1} = i \)
furthermore, \( \sqrt{-4} = 2i \)
i being equal to \(\sqrt{-1}\) has some interesting properties with exponents. Naturally exponentiation is the inverse of a root, that is \( 3^2 = 9, \text{ as } \sqrt{9} = 3 \text{ implies that } \sqrt{9}^2=9\) ,
When taken to negative numbers, we can see this effect, so \( \sqrt{-1}^2=-1 \text{ implies } \sqrt{-1}^2 = i^2 = i* i = -1\)
So what if we keep taking i to higher powers?
\( i * i = i^2 = -1 \text{ and } i * i * i = i^3 = -i \text{ and } i * i * i *i = i^4 = 1\) then this pattern repeats, so \( i^5 = i^4 * i = 1 * i = i \text{ and } i^6 = i^4 * i^2 = -1 \text{ and so on, } i^7 = -i, i^8 = 1, i^9 = i \) and so on.
While your initial reaction may be “Who cares?”, I assure you you’ll see the value of this in a bit.
ℂ - Complex Numbers #
Complex numbers then, the end of this adventure for most sane people, are just Real numbers with imaginary numbers, written together, so this is numbers like \( 32 + 4i \text{ or } 420.69 - 2i\) . This brings about something called the complex plane, as now if we want to plot these numbers we can no longer use a simple number line, but instead need an axis for each part, one for the Real (ℝ) part, and one for the imaginary part.
Here’s a video to help you understand imaginary and complex numbers, albeit it does assume you’ve at least seen both a little bit before.
Hypercomplex numbers are also a thing, this term includes Quaternions which are used in some very high level physics, but otherwise you’ll most likely never work with these.
Infinity #
Diving into the weeds for a bit, let’s poke the concept of Infinity:
Notation #
+, -, *, ÷, mod #
If you don’t know that addition, subtraction, multiplication, and division are, I think you’re in the wrong place…
That said, there are some things you may not be used to. For starters, multiplication can be written in a variety of ways. of course there’s the classic \( 2 \times 2 = 4 \) but you may also see \( 2 \cdot 2 = 4 \) or \( 2 * 2 = 4 \) or just \( 2(2) = 4 \) , where parentheses with no operation in between imply multiplication.
Typically, the \( 2 \cdot 2 = 4 \) and parentheses methods are used on paper, while the \( 2 * 2 = 4 \) is used on computer screens as it’s easy to type. \( 2 \times 2 = 4 \) is generally not preferred as it can be confused with other operations you’ll see later.
Something to keep in mind is that addition and multiplication are both commutative and associative, while subtraction and division are not. What this means is that while \( 2 + 3 = 3 + 2 \text{ but, } 2 - 3 \neq 3 - 2 \) (The Commutative Property) similarly, \( 2 * 3 = 3 * 2 \text{ but, } 2 \div 3 \neq 3 \div 2 \)
Furthermore, \( (2 + 3) + 4 = 3 + (2 + 4) \text{ but, } (2 - 3) - 4 \neq 2 - (3 - 4) \) and \( (2 * 3) * 4 = 3 * (2 * 4) \text{ but, } (2 \div 3) \div 4 \neq 2 \div (3 \div 4) \) , by the Associative Property.
Finally, for multiplication, you should keep in mind how to do multiplication on grouped items
[TODO] $a*(x+y)$ and $(a+b)(x+y)$ - FOIL
For division, there’s some terminology you should know. First of all, in \( \frac{a}{b} \) , a is the numerator and b is the denominator. The reciprocal of \( \frac{a}{b} \) is \( \frac{b}{a} \) . This is actually pretty useful, for example, given \( \frac{a}{\frac{b}{c}} \) you can write this as, \( a * \frac{c}{b} \)
Modulo is something you’ll see in programming a lot, in programming it’s usually represented with the percent sign.
Modulo is just the reminder after division, so 7%3 is 1, because 3 goes into 7 twice, with 1 left over.
^, √, !, log() #
exponents, written as either \( a^x \text{ or } \) a^x or exp(x) if the base is ’e’, that is \( e^x \) , are pretty simple to understand, they’re just repeated multiplication, so \( a^3 = a * a * a \)
This results in a few ‘rules’ for exponents which are fairly easy to understand, with the exception of the not at all intuitive \( a^0 = 1 \)
| Exponent Rule | Assume a≠0 and b≠0 |
|---|---|
| Product Rule | \( a^x * a^y = a^{x+y} \) |
| Quotient Rule | \( a^x / a^y = a^{x-y} \) |
| Power Rule | \( (a^x) ^y = a^{x*y}\) |
| Power of a Product Rule | \( (a*b)^x = a^x*b^x \) |
| Power of a Fraction Rule | \( (\frac{a}{b})^x = (\frac{a^x}{b^x}) \) |
| Fractional Exponent | \( a^{\frac{x}{y}} = \sqrt[y]{a^x} \) |
| Negative Exponent | \( a^{-x} = \frac{1}{a^x} \) |
| Zero Exponent ¡easy to forget! | \( a^0 = 1 \) |
alright, so why do I say these are intuitive? Let’s take the product rule for example. Let’s look at \( 2^2 * 2^3 = 2^5 \) this is true because \( 2^2 = 2*2 , 2^3 = 2 * 2 * 2 \text{, so multiplied together they're }(2 * 2) * (2 * 2 * 2) \text{ and as multiplication is associative that is } 2*2*2*2*2 = 2^5 \) , generally, any of these rules can be figured out by just writing out examples like these, expanding the exponent out like this, and seeing what happens.
Alright, so now we can look at roots. The most common root you’ll work with is the square root, which is what is implied when seeing a root symbol with no number in the crevice, though can be written explicitly as \( \sqrt[2]{n} \) , though as you should’ve notice in the exponent rules other roots are possible, for example the cube root, which is \( \sqrt[3]{n} \) is just whatever number you need to multiply with itself 3 times to get n, so for example \( \sqrt[3]{8} = 2 \text{ as } 2 * 2 * 2 = 8 \)
As implied by the Fractional exponent rule, roots can be written as fractional exponents, that is \( \sqrt[2]{n} = n^{1/2} \) often it’s actually more convenient to enter this notation into a calculator or programming language anyway. It can even just be nice for working on paper as when writing something like \( \frac{1}{\sqrt{ \text{some really long equation here}}} \) it can be easy to miss the top bar and forget it’s there, compared to \( \frac{1}{( \text{some really long equation here})^{\frac{1}{2}}} \) where the power sticks out more.
Next, there’s factorial, written with the !, it just means to multiply the number with the number prior down to 1, so \( 4! = 4 * 3 *2 * 1 \)
Finally, let’s look at Logarithms:
Scientific Notation #
Say you have a really big number like 2,340,000,000,000,000,000 or a really small number 0.000000567 in either case, writing out and counting the zeros is very cumbersome and easy to mess up. For this reason, scientific notation is common. In scientific notation, those numbers would be written as \( 2.34 \times 10^{18} \) and \( 5.67 \times 10^{-7} \) respectively. In each case, it’s just a matter of moving the numbers so that there’s only one digit before the decimal, then listing to what power of 10 you need to multiply this number by to get the original number- meaning the power will be the same as the number of 0’s in the original number. You may see calculators show this with a big ‘E’ instead of writing the \( x.xxxx \times 10^{y} \) , for example \( 5.67 \times 10^{-7} \) is often shown as 5.67E-7
[TODO] beyond scientific notation for REALLY big numbers video… numberphile?
=, <, >, ≤, ≥, ≠, «, », ≈, ∝ #
The equal sign is pretty obvious, it just means that what ever is on each side is equal. The implications of this will lead us deeper into algebra though as we actually solve equations. There’s some really obvious equalities, those that lack variables, so things like \( 1 + 2 = 3 \) or any of the equalities shown to this point really. Where equality gets a bit more interesting is when there’s an unknown (variable, same thing). For example, \( 1 + x = 3 \) here it’s pretty obvious that x must be 2. We’ll go into how to actually solve for these unknowns with non-obvious equations in a bit.
Less Than and Greater Than are similarly simple, they just state that one side has a bigger number than the other. The ‘>’ or ‘<’ symbols should always ’eat’ the bigger number, that is the open side faces the bigger number, and the pointy side points to the smaller. \( 2 < 3 \) and \( 4 > 3 \) are examples of this. When variable are involved, it usually means there are multiple solutions. \( x > 3 \) for example, is satisfied for any x greater than 3, right down to 3.0000000000…00001 all the way up to ∞. Similarly, there are ‘or equal to’ variants of less than and greater than, which are written with a bar underneath so \( x \geq 3 \) is satisfied for x equal to 3 to ∞, so the 3 is included with the ‘or equal to part.’
≠ means ‘Not Equal To’, and as the name implies it’s just saying the two sides can’t be equal so with \( x \neq 0 \) , x can be any value, except for 0.
Next are MUCH greater and less than, written with a double less than or greater than sign, so \( \gg \text{ or } \ll \) these are weird for people new to the idea, because they’re sort of fluid and depend on the situation. Generally they’re used to say “This number is so small that it doesn’t affect the outcome” or “This number is large that it dominates the outcome”
Next up, is ≈ or “Approximately Equal To”. This is for when you know your answer is off by some amount, due to imprecision in computation but it’s still close enough for whatever you need to use it for. For example \( \pi \approx 3.1416 \)
Finally, there’s ∝ for ‘proportional to’. This just means the two equations are only different by a multiplied constant. For example, say \( y = kx \) , where k is a constant (some number that can’t change) then \( y \propto x \) . This is useful for when two equations are representing something massively different in scale, but we want to indicate that they have the same behavior.
|x|, ∆, ⌊x⌋, ⌈x⌉, ± #
The \( |x| \) symbol means “Absolute Value”, which, is really just a fancy way of saying “Make it positive.”, so \( |3| = 3 \) , no change, but \( |-3| = 3 \) .
Delta, \( \Delta \) , is the change between two things, so from 10 to 20 degrees is a delta of 10 degrees. It is usually used with real units like this, giving us the difference between the final and inital values in an experiment. So really it’s just Final Value - Initial Value. You may also see \( \Delta t \) or \( \Delta x \) , this would be change in time and change in position (usually) respectively. Note that Δ can be negative.
\( \left \lfloor{x}\right \rfloor \) is the ‘floor’ of x. Similarly, \( \left \lceil{x}\right \rceil \) is the ‘ceiling’ of x. Very basically, for floor this just means to drop everything after the decmial right off, so \( \left \lfloor{1.534}\right \rfloor = 1 \) . For ceiling, it means to go up 1 and take the decimal off. \( \left \lceil{1.001}\right \rceil = 1\)
Finally, for lack of a better place to put it, let’s look at ±. This is ‘Plus or Minus’ and it just means to do both, for example 3±2 gives us 1 and 5 as answers. Usually when this symbol is used, one of the two answers ends up being thrown out as invalid, but not always.
f (x), (f ∘ g) #
[TODO]
(a,b), [a, b] #
[TODO]
∑, Π #
[TODO]
https://www.rapidtables.com/math/symbols/Basic_Math_Symbols.html
Order of Operations #
PEMDAS stands for Parentheses, Exponents, Multiplication, Division, Addition, Subtraction, and is in general the correct order to do math operations. so given a mess like \( \frac{4*(1 + 2)^3}{2+1} + 1 \) we can solve it in order. Here though, I have to point out the first failing in the PEMDAS acronym, division with a bar implies parentheses, as you’ll have to do the 2+1 on the bottom before you can do the divison anyway. That said, let’s look at this step by step
\[\frac{4*(1 + 2)^3}{2+1} + 1 = \frac{4*(3)^3}{2+1} + 1= \frac{4*(3)^3}{3} + 1 = \frac{4*27}{3} + 1= \frac{108}{3} +1 = 36+1 = 37\]In step 1 and 2 I did perenthes in top and the implied perenthes on the bottom, then in step 3 I did the exponent, followed by the multipliation and divison in steps 4 and 5, finally in the last step I did the +1 that was hanging off the entire time.
The P for Perenthes in PEMDAS can mean really any grouping symbol, so brackets [] or braces {}, whatever.
So, what’s the problem with the math equation in the start and why do people disagree? Well, Divison and Multiplication don’t have to be done in that order, same for addition and substraction, instead they should be done all together, but going from left to right, so \( 1 + 2 + 3 - 4 + 1 - 2 \) for example can be done in order left to right giving us 1, not doing this: \( (1 + 2 + 3) - (4 + 1) - 2 \) which gives -1. Just to be crystal clear, 1 not -1 is correct here. So, applying this to the above social media meme, it’s the same problem but with multiplication, implied with the 3(3) after doing the addition, and the divison. Some people interpret PEMDAS literally, meaning multiplication is done before division always. These people are wrong. So, with the meme the problem looks like this:
\[\frac{6}{3(1+2)} = \frac{6}{3(3)} = \frac{6}{9} = \frac{2}{3}\]But see what I did there? I wrote the fraction as a bar, not as ÷, and here, because this problem is written crappily, that actually changes the solution! And I know what you’re thinking- Division is divison, how could that matter?? And you’re right, it is. It matters because the bar implies that order, but if I go back to using a division sign look what happens:
\[6\div3(1+2) = 6\div3(3) = 2(3) = 6\]And there’s the problem. Now, you’re probably thinking “What fucking dipshit let math be ambiguous?” and the answer is really that this problem is just stupid. In any real problem the ambiguity here should be fixed by whoever is writing it in the first place, and since other than in textbooks math doesn’t just appear from thin air, the true order of the operations should be specified clearly with parentheses, either as:
\[6\div(3(1+2))) \text{ -OR- } (6\div3)(1+2)) \text{ -OR- } \frac{6}{3(1+2)}\]where in the last option the bar implies the parentheses.
Simplification #
[TODO] redo with https://github.com/airladon/FigureOne
Before we can get to doing useful things with these operations, it helps to be proficient at simplifying an equation. For example say we have:
\[ 3x^2+3+(2-x)(4-x)+2=12+(3+(x*2))+2\] Before we ever solve for x, we’ll want to turn this into something much easier to work with. When doing this, we need to make sure to keep the equality the same, that is if we had \(3+x=4\) we need to not accidentally change it into \(3+x=5\) , changing the answer.
This generally means that we can only either do basic operations to get an equivalent value or do the same operation to both sides. Ironically, often simplification actually requires expansion first, that is doing math like the \((2-x)(4-x)\) to get \(8-2x-4x+x^2\) which can then be reduced back down to \(x^2-6x+8\) .
For the example equation, the most obvious thing to start with is the +2 that’s common to both sides. This is our first example of using the same operation on both sides- the idea being as long as we apply the same operation on both sides of the equality the meaning won’t change. That is, the solution to \(x+3=2\) is the same as the solution to \(x+3+2=2+2\) , but we can take advantage of this to get rid of terms too. For example, with \(x+3=2\) we can subtract 3 from both sides to get \(x=-1\) (seeing how this might lead to solving the equation?) In our example equation, both end in a +2 so we can “cancel this out” by subtracting 2 from both sides.
\[\begin{aligned} 3x^2+3+(2-x)(4-x)+2&=12+(3+(x*2))+2 \\ 3x^2+3+(2-x)(4-x)&=12+(3+(x*2)) \end{aligned} \]but because we did the same operation to both sides of the equality, the answer didn’t change
☠☠☠ The following is an easy place to screw up ☠☠☠
Keep in mind, whatever you do you need to do to both sides and the entirety of both sides, not just one term. For example, If you were to only divide one term on each side by 2 this is not keeping equivalence. You can divide both sides in full by two, sure, but you can’t just pick one term from each side and selectively divide that term by two. That is \(4+2x=8\) can become \(2-x=4\) but not \(\frac{4}{2}+2x=\frac{8}{2}\) which is \(2+2x=4\) . You can see this as the solution to \(4+2x=8\) is \(x=2\) but the solution to \(2+2x=4\) is \(x=1\) . So, just be sure if you do some arbitrary operation you do it to both sides and the entirety of the side, not just one term.
Back to our big equation: next, let’s FOIL out that \((2-x)(4-x)\) …
\[\begin{aligned} 3x^2+3+(8-2x-4x+x^2)&=12+(3+(x*2))\\ 3x^2+3+(x^2-6x+8)&=12+(3+(x*2)) \end{aligned} \]with that done, we can get rid of some of those parentheses
\[3x^2+3+x^2-6x+8=12+3+2x\]then, we can combine like terms,
\[4x^2-6x+11=15+2x\]and subtract \(2x\) from both sides
\[\begin{aligned} 4x^2-6x-2x+11&=15+2x-2x\\ 4x^2-8x+11&=15 \end{aligned} \]then subtract 15 from both sides
\[\begin{aligned} 4x^2-8x+11-15&=15-15\\ 4x^2-8x-4&=0 \end{aligned} \]And now we’re fully simplified. You can’t combine the \(x^2\) and x terms.
This general process applies to any equation. It’s like a little puzzle, you just want to take the complex equation you have, do the same thing to both sides or do the math that’s internal to one side. Sometimes it’s more complicated to do this. For example, you might need to square root both sides to “cancel out” both sides being squared, for example \(x^2=25\) to \(\sqrt{x^2} = \sqrt{25}\) to \(x=5\) , but here this only works because we’re square rooting everything on both sides.
Plotting functions #
[TODO]
‘Plotting’ on Algorithm Archive
Looking at some equations #
Linear #
[TODO] replaces these desmos graphs with something custom using https://jsxgraph.uni-bayreuth.de/wp/index.html
it’ll be uglier, but I don’t like loading something this large, and jsxgraph will be more flexible anyway. Since I literally never write js this is proving to be a bit rough. Working on getting something that will show the slope and intercept values as two arbitrary points on the line are moved on a graph.
|
|
is what I have so far, but it appears the .X and .Y getters are not working as I expect. This should give me an ‘S’ point that I can then line segment to A and B to get the right angle ‘stair’ step slope.
Polynomials #
Parabolas #
Systems of Equations #
Nobody should do these by hand unless they’re dead simple
Imaginary numbers, systems of equations
1¼ - Accuracy and Precision #
For lack of a better place to put it and not wanting to wait until the much latter section on probability, I’d like to briefly mention the difference between Accuracy and Precision. Typically, this is represented as
1½ - Coordinate Systems #
So, up until now you’ve only seen the XY ‘Cartesian’ coordinate system, but I did gloss over some details. For starters, when refering to points in the Cartesian plane, you may hear the term quadrants, these are the 4 infinite corners of the plane, coming out from the ‘+’ shape at (0,0). Slightly counter intuitively, they’re numbered from starting in the top right and going counter clockwise.
[TODO] picture here
The Cartesian coordinate system can be expanded into high dimensions as well, but you’re unlike to work with more than 3, to form space defined with XYZ
[TODO] picture here
There are a few other coordinate systems you’ll likely come across though: Polar, Cylindrical, and Spherical.
[TODO] all 3 of those
1¾ - Primes & Factors #
Alright, so maybe not something you’ll use everday, but you still should know the basics of primes, especially if you want to understand Public-key cryptography. So, what’s a prime?
A prime is a number where the only two whole numbers that you can multiply to get to that number are 1 and itself.
2? Prime. 1*2 is the only option.
3? Prime. 1*3 is the only option.
4? Not Prime. 2*2 = 4, as does 1*4
103801? Prime. only two numbers that can multiplied together to get it are 1 and 103801.
I think you get the gist. One of the neat applications of primes is that multiplying two prime numbers together makes for a number that’s not quite prime, but whose only other factors are two numbers that you multiplied together, so say we take 103801 * 7 to get 726607, the only two whole numbers other than 1 and itself that can be multiplied to get 726607 are 103801 and 7.
There are also ‘antiprimes’ (or ‘highly composite numbers’), from Wikipedia:
… an antiprime number, is a positive integer with more divisors than any smaller positive integer has
so, technically 1, 2, 4, and 6 are all antiprime. But where it gets interesting is with larger numbers. For example, 360 is anti prime as you get to it with \( 2*2*2*2*3*3*5\) , which is 7 primes multiplied together, more than it takes to get to any number prior. These numbers are really easy to work with because of this, and it makes it really convenient for the number of degrees in a circle as it can be divided so easily.